including WordPress, SquareSpace, Joomla, Drupal, Magento, and Unbounce.
- Unbounce

- Wordpress

- Drupal




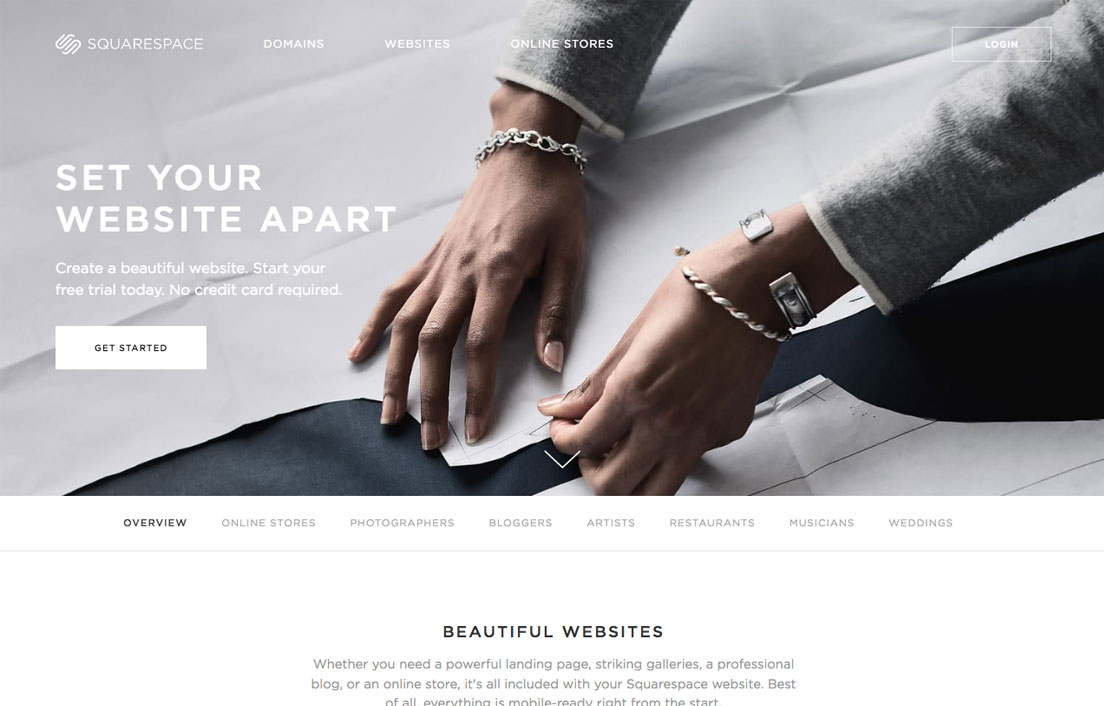

- Squarespace

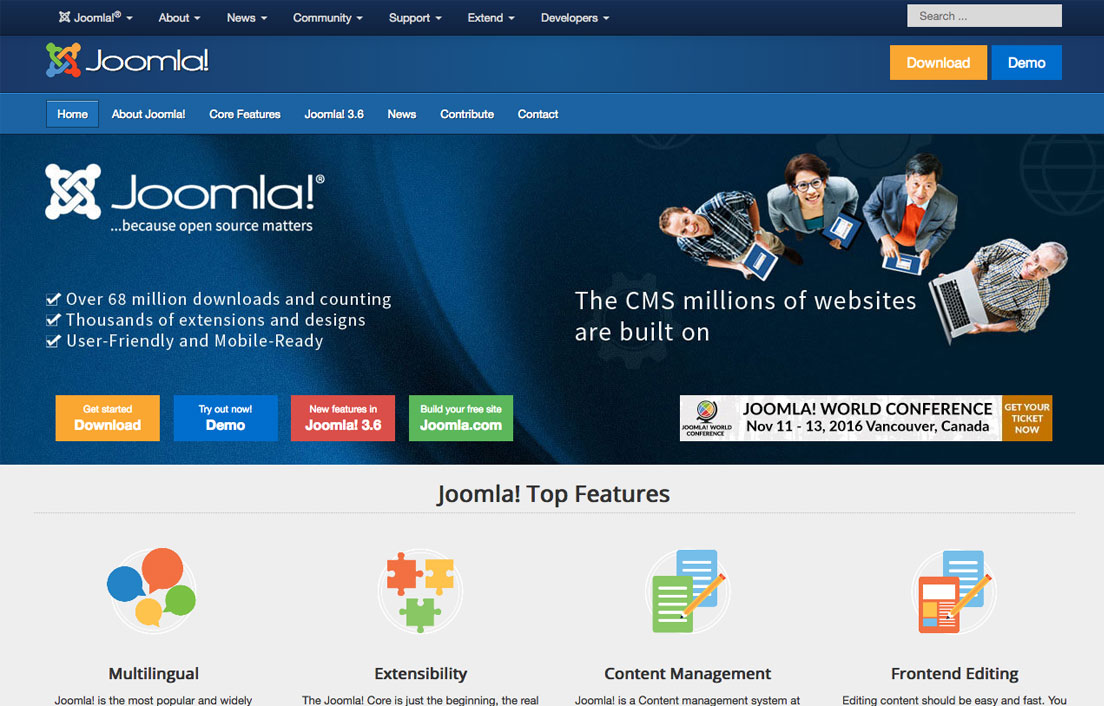
- Joomla

- Magento

力学中,一夹子夹住木块在力 f 作用下向上提升的过程呈现出丰富的物理现象,值得深入探讨。
* 当夹子静止时,木块受到夹子向上施加的力、自身的重力以及与地面的支持力。由于木块处于静止状态,所以这些力处于平衡状态。
* 因此,力平衡方程为:f - W = N,其中 f 为夹子施加的力,W 为木块重力,N 为地面支持力。
* 由于夹子是固定在墙上的,所以夹子不会移动,其受到的力平衡方程为:R - f = 0,其中 R 为墙对夹子的反作用力。
* 当木块在夹子作用下上升时,夹子对木块做功,使木块获得动能。
* 根据能量守恒定律,夹子对木块做的功等于木块获得的动能:W = ΔK,其中 W 为夹子做的功,ΔK 为木块动能的变化量。
* 夹子做的功等于 f 乘以木块上升的高度,而木块动能的变化量等于 1/2mv2,其中 m 为木块质量,v 为木块上升的速度。
* 在夹子作用下,木块向上做加速度运动。
* 木块加速度大小可以用牛顿第二定律求得:a = f/m,其中 a 为木块加速度,f 为夹子施加的力,m 为木块质量。
* 根据加速度运动公式,木块上升速度可表示为:v = at + v?,其中 t 为时间,v? 为初始速度(通常为 0)。
* 当木块与夹子接触时,会产生摩擦力。
* 摩擦力方向与木块运动相反,阻碍木块上升。
* 摩擦力大小与夹子与木块之间的接触面积和接触力成正比,可用 μN 表示,其中 μ 为动摩擦因数,N 为接触力。
* 当夹子夹住木块时,夹子会发生形变,存储弹性势能。
* 当夹子释放木块时,弹性势能会转化为木块的动能。
* 弹性势能为:U = 1/2kx2,其中 k 为夹子的弹性系数,x 为夹子的形变量。
* 夹子对木块做的总功等于克服木块重力所做的功、克服摩擦力所做的功和克服空气阻力所做的功之和。
* 夹子的效率等于有用功除以总功,可以用 η = W полезная / W 表示,其中 W полезная 为有用功,W 为总功。
* 当夹子突然释放木块时,木块会由于惯性而继续向上运动。
* 惯性力大小等于木块质量乘以木块加速度,方向与木块加速度相反。
* 惯性力在很多运动现象中都有表现,例如物体被抛出后仍继续运动。
* 对木块做加速度运动的描述取决于所选的参考系。
* 在以地球为参考系的观察者看来,木块在上升;而在以木块为参考系的观察者看来,木块是静止的,而地球在下降。
* 选择适当的参考系有助于解决许多物理问题。
* 在进行一夹子夹住木块向上提升的实验时,需要采取适当的安全措施。
* 夹子使用的力不宜过大,以免损坏木块或夹子。
* 实验区域应保持安全,避免木块或夹子掉落伤人。
* 一夹子夹住木块向上提升的过程可以延伸到许多实际问题中。
* 例如,汽车的悬挂系统利用弹簧的弹性势能来吸收震动,使汽车平稳行驶。
* 了解一夹子夹住木块向上提升的原理对理解许多机械装置的运作原理至关重要。
-











